浅谈模态参与因子和模态有效质量

模态分析是研究结构的动态特性的主要方法之一，通常应用在工程振动领域。通过模态分析主要可以得到结构的固有频率、阻尼比和模态振型。分析这些模态参数的过程称为模态分析。对于一个n自由度系统，理论上存在n个模态，然而在这些模态中哪些模态对结构的响应起主要作用，通常使用模态有效质量来判定。

将实际的结构通过有限元法离散化处理后，其广义动力学方程可表达为：

其中M为结构的质量矩阵，C为结构的阻尼矩阵，K则为刚度矩阵，F(t)为外载荷激励。通常模态计算时不考虑外部载荷，即F(t)=0，在此基础上，忽略结构阻尼后，广义动力学方程可表达为：

通过求解二阶齐次微分方程，可以得到上式的特征值和特征向量。由此可得到结构的固有频率ω及振型函数Φ，其中：

设定Φ为结构模态特征值向量，在有限元中按照质量归一化或者刚度归一化或者最大幅值归一化的原则，对质量进行归一化处理，结构的广义质量矩阵可表达为：

模态参与因子是一种描述模态和某一向量激励相互作用关系的参数，为每个质点质量与其在某一振型中相应坐标乘积之和与该阶振型模态质量之比，因此模态参与因子的表达式为：

模态有效质量就是按照模态质量归一化后求得的模态参与因子的平方和，其表达式为：

在某一向量的激励下，每阶模态都存在相应的模态有效质量，有效质量大的更容易被激励起来，因此通过模态有效质量可以判定各阶模态的重要性。

案例：基于Marc软件的悬臂梁模态分析及模态有效质量提取

本案例使用Marc 2022版本对悬臂梁结构进行约束模态分析，系统一阶固有频率及振型图如下所示：

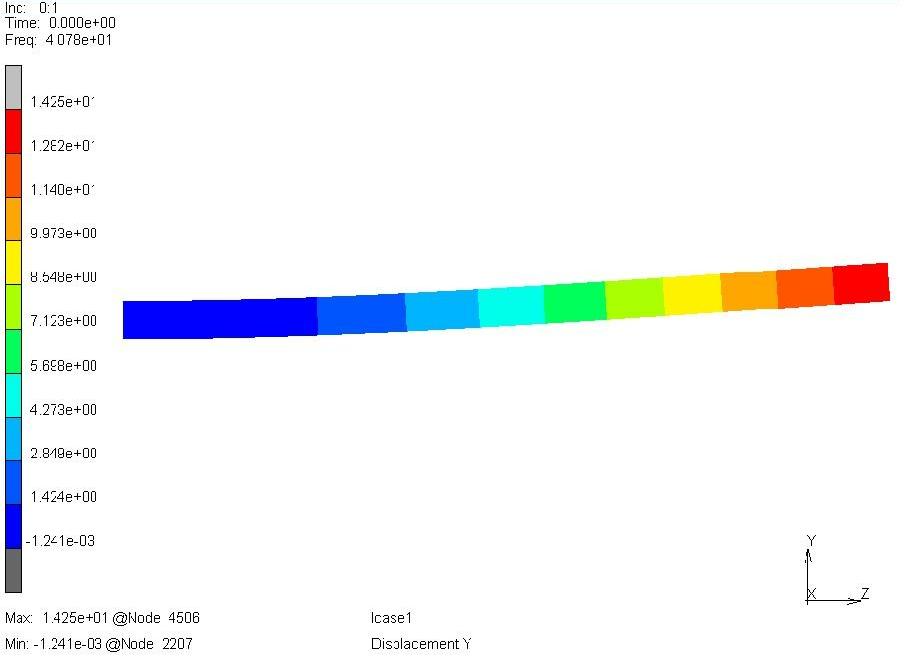
系统一阶固有频率为40.7839Hz，对应的模态参与因子和模态有效质量如下图所示，在各方向上的模态有效质量分别为对应方向上模态参与因子的平方和。